Diferensiasi fungsi trigonometri

Diferensial Trigonometri 

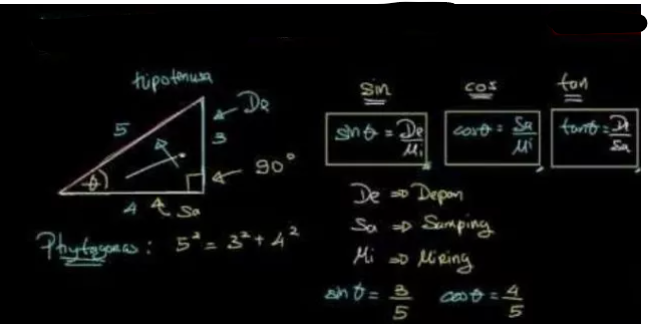
.1. Pengenalan Trigonometri 

.2. Diferensial Trigonometri 

.3. Diferensial Invers Trigonometri

Diferensiasi fungsi trigonometri atau turunan fungsi trigonometri adalah proses matematis untuk menemukan turunan suatu fungsi trigonometri atau tingkat perubahan terkait dengan suatu variabelnya. Fungsi trigonometri yang umum digunakan adalah sin(x), cos(x) dan tan(x).

Sedangkan turunan yaitu laju perubahan suatu fungsi terhadap perubahan perubahnya. Perlu diketahui, turunan f(x) ditulis f'(a) dimana tingkat perubahan fungsi ada pada titik a.

Jadi turunan trigonometri merupakan proses matematis guna memperoleh turunan pada sebuah fungsi trigonometri.

Sementara f' (dibaca f aksen) dapat disebut sebagai suatu fungsi baru. Pada fungsi trigonometri yang biasanya dipakai yaitu sin x, cos x, dan tan x.


Rumus Turunan Fungsi Trigonometri
 
1.  f(x) = sin u  →  f ‘(x) = cos u . u’
2.  f(x) = cos u  →  f ‘(x) = −sin u . u’
3.  f(x) = tan u  →  f ‘(x) = sec2u . u’
4.  f(x) = cot u  →  f ‘(x) = −csc2 u . u’
5.  f(x) = sec u  →  f ‘(x) = sec u tan u . u’
6.  f(x) = csc u  →  f ‘(x) = −csc u cot u . u’

 Contoh Soal 1

Tentukan y' dari y = -2 cos x

Jawab:

y = -2 cos x

y' = -2 (-sin x)

Maka, y' = 2 sin x

Contoh Soal 2

Tentukan y' dari y = 4 sin x + 5 cos x

Jawab:

y = 3 sin x + 5 cos x

y' = 3 (cos x) + 5 (-sin x)

Maka, y' = 3 cos x - 5 sin x

Contoh Soal 3

Tentukan y' dari y = 4 cos x - 2 sin x

Jawab:

y = 4 cos x - 2 sin x

y' = 4 (-sin x) - 2 (cos x)

Maka, y' = -4 sin x - 2 cos x

2. Diferensial Trigonometri /Turunan Fungsi Trigonometri

Turunan fungsi trigonometri diaplikasikan dalam bidang matematika dan kehidupan nyata, berikut diantaranya:

Menentukan kemiringan garis singgung kurva trigonometri y = f(x)

Menentukan kemiringan garis normal terhadap kurva trigonometri y = f(x)

Menentukan persamaan pada garis normal kurva dan garis singgung

Turunan fungsi trigonometri dapat dimanfaatkan di berbagai bidang seperti elektronik, pemrograman komputer, dan pemodelan fungsi siklik yang berbeda

Menentukan nilai maksimum dan minimum dari fungsi tertentu.

 7. Rumus : Turunan y = [u(x)]n 

                  y′=n[u(x)]n−1.u′(x)

Contoh 4 Tentukan turunan dari y = cos⁵6x

Contoh 5  Tentukan turunan dari    u(x) = cos ⁶x  

Contoh 6 Tentukan turunan dari y = sin⁶(3x−1)        

Latihan 7Tentukan turunan dari y = sin x²

Latihan 8 Tentukan turunan dari y = cos (3x+1)
 Latihan 9 Tentukan turunan dari f(x) = tan 12x

Latihan 10 Tentukan turunan y = sin (x2+3x−1)

Latihan 11 Tentukan turunan dari y = sec 2x

Latihan 12 Tentukan turunan dari y = cos (2x+1⁾⁴

Latihan 13 Tentukan turunan dari y = tan⁵3x         
Latihan 14 Tentukan turunan dari y = cos⁴(5x+2)

Latihan 15  Tentukan turunan y = sin⁶(x2+3x)

Latihan 16 Tentukan f ‘(x) dari :

a.  f(x) = 3sin 2x + 4cos x
b  .f(x) = tan 2x − csc x
c.  f(x) = sec 4x + tan (x+1)
 

Latihan 17 Tentukan turunan dari y = x²cos 2x

 Latihan 18 Tentukan turunan dari f(x) = (1 + sin2x)⁷

3.Diferensial Invers Trigonometri

Fungsi Trigonometri Invers

Berdasarkan ide fungsi invers, fungsi-fungsi trigonometri juga memiliki invers, hanya saja perlu dibatasi domainnya. Pembatasan domain ini penting untuk menjamin bahwa fungsi tersebut benar-benar memiliki invers.

Yang dimaksud dengan invers trigonometri adalah balikan dari fungsi trigonometri

y = sin x maka x = arc sin y

y = cos x maka x = arc cos y

y = tan x maka x = arc tan y

y = cot x maka x = arc cot y

y = sec x maka x = arc sec y

y = csc x maka x = arc csc y

 

Artinya

arc sin 1 = 90o

arc sin 1/2 = 30o

arc tan 1 = 45o

dan sebagainya